At the moment exists a lot of methods for calculating the famous \(\pi\) number, but in this post, we use a basic and quick method.
In the next figure, we see a circle circumscribed on a square. If we calculate the ratio area of the circle on the square we get: \[ \frac{\textrm{circle area}}{\textrm{square area}} = \frac{\pi (\frac{a}{2})^2}{a^2} = \frac{\pi}{4} \]
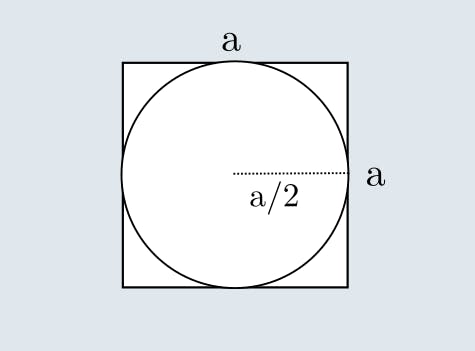
The next phase is to approximate this by the Montecarlo method, this method is useful when we need approximate complex expressions using probability, for example, if we paint random points in this image we get: \[ \frac{\textrm{number of points in circle}}{\textrm{all points}} \sim \frac{\pi}{4} \]
Programing
I created a notebook in jupyter that describes the process of the algorithm.
We approximate Pi value using Montecarlo method.
Initializing libraries and objects
from collections import namedtuple
from math import sqrt
from random import random
Point = namedtuple('Point', 'x y')
Defining the euclidean distance.
def distance(point: Point, other_point: Point):
return sqrt((point.x - other_point.x)**2 + (point.y - other_point.y)**2)
distance(Point(0, 0), Point(3, 4))
5.0
Creating random points
RANDOM_POINTS_NUMBER = 999999
points_lists = []
for _ in range(RANDOM_POINTS_NUMBER):
points_lists.append(Point(random(), random()))
points_lists[:10]
[Point(x=0.1612926124022096, y=0.060923049944938024),
Point(x=0.6270887477998938, y=0.44092407685036095),
Point(x=0.7626921170940966, y=0.050805039626968806),
Point(x=0.2813947208789642, y=0.4423323656719348),
Point(x=0.45424479957922936, y=0.8615366921729465),
Point(x=0.2870610688184644, y=0.20637975674444264),
Point(x=0.715345600601381, y=0.316279124793049),
Point(x=0.06997887187154217, y=0.45592397256213724),
Point(x=0.051783287833011005, y=0.4292635246979777),
Point(x=0.07879622453659263, y=0.5470782237556773)]
To classify if a point is inside the circle, we calculate the distance of the point to the center of the circle and if it is smaller to the radius then the point is inside the circle.
circle_points = []
for point in points_lists:
if distance(point, Point(0.5, 0.5)) < 0.5: # The point are in the circle
circle_points.append(point)
len(circle_points)
785360
The ratio of the points in the circle and all points is the same as the ratio of the area of the circle and area of the square, i.e. \(\pi/4\).
print(len(circle_points)/RANDOM_POINTS_NUMBER)
print(4 * len(circle_points)/RANDOM_POINTS_NUMBER)
0.7853607853607854
3.1414431414431414
Voilà we approximated the value of \(\pi\)
The code of the notebook is here Python notebook